钟义信的全信息理论存在的问题

 鲁晨光

辽宁工程技术大学数学和人工智能学院，中国阜新

长沙学院计算机工程和应用数学学院，中国长沙

摘要：钟义信的专著《信息科学原理》核心部分是全信息理论——它发扬Weaver的信息三个层次思想，提供了语法、语义、和语用信息公式，这些测度公式存在不少问题，包括：说错说对信息一样多，信息量和逻辑概率无关，和香农信息论相差太远，很难用来度量日常生活中的语义信息，也很难用于机器学习。文中讨论了这些问题存在的原因(研究路线特殊等)，同时比较了作者的研究路线和语义信息公式。

关键字：信息科学，语义信息论，语义信息测度，语用信息

                  作者简介

鲁晨光，男，1955年8月生，曾任长沙大学计算机系副教授，长沙青年学术带头人。曾在加拿大尼亚加纳学院接受培训并在北师大数学系做访问学者。现为辽宁工程技术大学客座教授。主要研究兴趣是：语义信息论、机器学习、色觉机制、投资组合、美感和进化。提出色觉机制的译码模型和广义信息论 （即语义信息论）。于《通信学报》、《光学学报》、Int. J. of General Systems, Entropy、Information 等国内外期刊发表约40篇论文；出版学术专著4部。Email: lcguang@foxmail.com。

个人主页：http://survivor99.com

1.      序言

钟义信曾任中国信息论学会和人工智能学会主席，其《信息科学原理》【1】作为多所高校的教材，已经出到第五版，影响巨大。钟义信的信息科学的核心部分是全信息理论，这一理论遵照Weaver关于信息三个层次的思想(【2】，p.96)，把量化三种信息(语法信息、语义信息和语用信息)作为该理论的核心内容。其最近论文【3】叙述略有不同，但是主要公式基本相同。最近，我看到李宗荣和田爱景的文章【4】,其中批评说：以量化为核心的全信息理论作为信息科学的基础理论不妥，这是用广义信息论冒充信息科学。我的看法不同，我认为：虽然量化不是充分的，但却是必要的；不是量化走偏了，而是钟义信的量化有问题。本文想澄清这些问题。

我认为，钟义信对中国的信息科学促进很大，特别是他超前地倡导语义信息论研究，倡导信息科学和人工智能相结合。我的研究就遵循他倡导的方向【5,6】。但是，他的权威性也使得全信息理论无人质疑。另一方面，因为全信息理论很难应用，跟随者几乎没有。连同是北邮的牛凯和张平发表的长文《一个语义通信的数学理论》【7】也没有引用钟义信的文章或著作。这种没有学术比较和争论的学术环境太不正常了。

2. 全信息理论简述

我首次见到钟教授是在1989年青岛的信息论年会上，他把香农熵和Deluca-Termini模糊熵相加定义为全信息熵，用先验熵减去后验熵就得到全信息，包括语义信息。后来在信息科学原理一书中，他加进了语用考虑。一个语句y的语义和语用描述可以表示为：

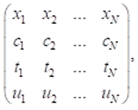
其中x_i是随机事件X的取值, c_i是相应x_i的肯定度，其最大值是1。肯定度c的分布一般不是归一化的。t_i是y相应x_i的真值，u_i是相应x_i的效用。x_i发生时，y提供的语法信息就是(见【3】的附录)：

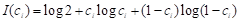,                      (1)

平均语法信息(量)就是

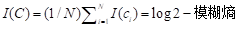,                       (2)

其中log2是最大可能模糊熵。平均模糊信息就是模糊熵的减量。log2也可以被先验模糊熵取代。上式之所以用到c_i和1–c_i, 是因为c₁+c₂+…c_n≠1(c不是归一化的), 而c_i+(1–c_i)=1。

如果我们用t_i取代上式中的c_i，语法信息(量)就变成单纯语义信息(量)，即

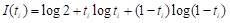,                                (3)

如果我们用c_it_i取代上式中的c_i，语法信息就变成综合语义信息，即

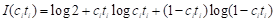,                            (4)

如果我们用u_i代替c_i,语义信息就变成单纯语用信息。如果我们用c_it_iu_i代替c_i，语法信息就变成综合语用信息:

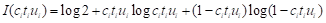.                (5)

平均语法信息是

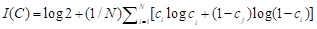.                    (6)

平均语义信息I(T)和语用信息I(U)同理。

假设c是先验肯定度分布，c*是后验肯定度分布，则相对语法信息就是(【1】, p.131):

I(C, C*; R)=I(C*) – I(C) = 先验模糊熵–后验模糊熵.                   (7)

其中R表示主体，意味着信息是相对的。同理，有相对语义信息I(T, T*; R)=I(T*)–I(T)和相对语用信息I(U, U*; R)= I(U*)–I(U) (【1】，3.4节)。 根据这些公式，模糊熵减小了，相对信息就是正的; 否则相对信息是负。

 如果c是归一化的，比如c是x的概率分布P(x), 语法信息被定义为(【1】, p.129):

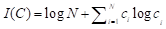.                                          (8)

设I(C*)是后验分布c*提供的信息，则相对语法信息(平均信息的增量)是I(C*)–I(C). 如果c*是0-1分布，则相对信息等于log2–I(C)=H(X)(【1】，pp.129-130)。由此可以得出香农熵是相对语法信息的特例。我想提醒：当c归一化时，我们并不能用c_it_i或c_it_iu_i代替c_i, 放进式8，得到综合语义信息和综合语用信息。因为两个或3个分布函数(最大值是1)的乘积并不是归一化的，不能放在log左边用以求平均。

在钟义信的最近文章【3】中叙述有所不同，他用y_i表示第i个semantic information(似应说message)，其真值是t_i. y提供的语义信息就是I(y_i)=I(t_i)。从他的y_i的用法看，y_i就是x_i发生时的命题y(x_i), t_i就是该命题的真值。这样理解，两种叙述就不矛盾。

3.举例说明全信息公式存在的问题

3.1 计算一个简单例子的语义信息量

假设有“老年人”标签或语句(命题函数或谓词)“这是老年人”(记为y₁)，人的年龄是x。考虑y₁提供关于x的语义信息。按照常识，如果x真的是老年人，比如70岁，信息就多；否则(比如x=10)，信息就少。

我们看公式3是否符合这个要求。

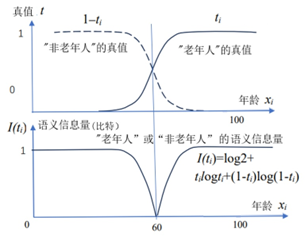
图1. “老年人”的真值函数和语义信息量——按钟义信的语义信息公式

可见I(t_i)不能保证说对了信息就多，说错了信息就少；而是说对了或者说反了，信息一样多。I(t_i)最小值是在x=60时, 即真值是0.5的时候。可见I(t_i)反映的不是语义信息量，而是语言清晰度。

另外，按照Popper的理论，逻辑概率越小，语义信息量越大。逻辑概率就是一句话被判断为真的概率。比如y₂=“成年人”，其逻辑概率就是大于或等于18周岁的人的出现的概率，大约是0.7。“老年人”没有明确外延，但是可用Zadeh计算模糊事件的概率的公式计算。无论外延清晰与否，隶属函数或真值函数的平均值就是逻辑概率【6】。所以老年人的逻辑概率小些，大概是0.25. 如果y₁和y₂同样正确，y₁提供的语义信息量更大。

有比较才能更好鉴别。按照我的语义信息G理论【6】，语义信息量公式是：语义信息量=log(真值/逻辑概率). 参看图2.

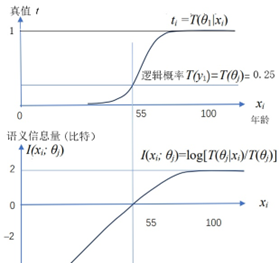
图2. 鲁晨光的语义信息G理论中的语义信息量公式

上面公式既考虑真假，也考虑了逻辑概率T(θ_j)。如果说错了，语义信息就是负的。这符合常理。因为失真函数d(x, y_j) = –logT(θ_j|x), 所以

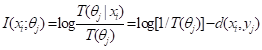.                         (9)

如果真值总是1，上面公式就变成Carnap和Bar-Hillel的语义信息量公式【8】。可见最大语义信息准则等价于机器学习常用的正则化最小失真准则。如果给定y_j时x发生的条件概率是P(x|y_j)，则根据语义贝叶斯公式【6】，有平均语义信息公式：

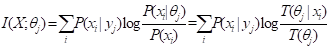.              (10)

这一公式可以保证在P(x|θ_j)=P(x|y_j)或T(θ_j|x)∝P(y_j|x)时(即语义信道匹配香农信道时)，I(X; θ_j)达最大，等于Kullback-Leibler(KL)信息。上式也显示了最大语义信息准则等价于最大似然准则。再对不同的y_j求平均就得到语义互信息。

下面我们联系上面例子看钟义信的语义信息公式存在的问题。

3.2 问题1：不符合常理

钟义信的语义信息公式不符合常理表现在：

1)命题无论真假，信息一样多

我们本希望，一句话或一个命题，说对了信息多，说错了信息少，甚至是负的，但是无论是t_i=0还是t_i=1, I(t_i)=I(1–t_i)不变。t_i换成c_i, u_i, c_it_i, c_it_iu_i，有同样问题(参看式1，3-5)。这说明该语义信息公式不能用于预测评价和事实检验。

2)语义信息量和逻辑概率无关

如果我们把“老年人“换成“上百岁老人”就能看出，其肯定句和否定句提供的语义信息量大为不同。按常理，说“来人不是上百岁的老人”几乎总是正确，提供的信息几乎是0；而说“来人是上百岁老人”，如果是对的，信息量极大，因为其逻辑概率极小。钟义信的语义信息公式和逻辑概率无关，这既不符合Popper和Carnap等人的思想，也不符合常理。

3.3 问题2：公式“信息=先验熵–后验熵”没有理论依据

钟义信的论证中频繁地使用了公式：信息=先验熵–后验熵。据此，假设先验和后验概率或肯定度分布是c和c*，信息或相对信息就是H(C)–H(C*)。这里H( )是香农熵或模糊熵。然而，这个公式没有理论依据。考虑x的先验概率分布是P(x),后验概率分布是P(x|y_j)，似乎有信息：

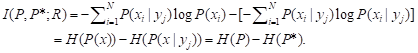        (11)

其中P是P(x), P*是P(x|y_j). 然而，这是不对的。香农理论中有互信息公式：

I(X; Y)=H(X)–H(X|Y),                                     (12)

其中H(X|Y)是条件熵，不是后验熵(即后验概率分布P(x|y_j)的熵)，因为对数左右的函数可能不同。当Y=y_j时，上式变为：

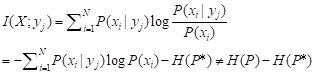            (13)

只有先验概率分布是等概率时，即P(x)=1/N时，才有I(X;y_j)=I(P,P*;R)=logN–H(P*).

I(X;y_j)和I(P,P*;R)的差别是：

1)I(X; y_j)是Kullback-Leibler信息，总是大于0；而H(P)–H(P*)可能小于0；

2)I(X;y_j)反映因为预测而节省的平均码长，而I(P,P*;R)=H(P)–H(P*)反映对两个不同信源编码的平均码长之差。前者才是y_j提供的信息。后者导致负信息也不是因为主观预测错了，而是客观的概率分布变了。所以H(P*)–H(P)不能用来评价预测好坏或度量信息。

3.4 问题3：说香农信息是全信息的特例不能成立

式8其实是用香农熵定义c归一化时的语法信息，因为logN就是P(c)=1/N时的香农先验熵，后面部分是负的香农熵，KL信息就是

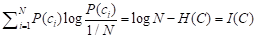.                    (14)

钟义信在定义了式8之后，又假设P(c)是等概率的，得到I(C)–I(C*)=H(C)=H(X)【1】(P. 130))。可见，特例不是推导出来的，是强行定义的。

在通常的信息论研究中，信息是熵(先验熵)和条件熵之差，但是在全信息理论中，香农熵是两个语法信息量之差。如果要得到香农互信息，是不是要使用两对语法信息之差？简单问题搞复杂了。

3.5 问题4：语用信息定义太主观，含义不明

关于效用的信息有多种：1)联系到效用，比如涨工资信息；2)关于目的信息或目标定向信息(即反馈信息)，比如定位地图提供的信息——告诉目的地还有多远；3)能带来效用增量或价值的信息，比如股市涨跌预测提供的信息。无论那种，信息也还是香农信息或语义信息，只是和效用相关。

研究语用信息一般是研究如何度量信息带来的效用和价值，比如Arrow 【9】，Cover 【10】和我【11】都用投资组合作为例子研究如何度量信息的效用和价值。信息的效用是根据预测优化投资比例时资本的回报率R*(1+利润率）。如果新的预测提供的信息使得改进的投资组合回报率是R**，则信息价值是log(R**/R*)的平均值。尽管大家结论不同【6】，但是基本思想是一致的，那就是：信息价值公式有实际投资意义，应当能够用来优化投资组合。而钟义信的语用信息公式有什么实际意义，令人费解。

因为I(u_i)和I(t_i)类似，预测反了I(u_i)一样多，所以I(u_i)也不符合常理。

3.6 问题5：缺少信道容量和语义压缩考虑

香农信息论提供了信道容量公式和信息率失真函数，用于优化信息传输和和数据压缩。钟义信的全信息理论只提供了信息度，其真值函数可看做语义信道，但是他没有考虑语义信道容量。因为他没使用条件概率和香农信道，所以也没有考虑两种信道相互匹配——这是语义信息论用于解释机器学习最有价值的地方【6】。其他语义信息论【6,12】都提出用于优化语义压缩的推广的信息率失真函数(我的G理论中是R(G)函数); 全信息理论也没有考虑语义压缩。所以全信息理论作为一个信息理论是不完整的。

3.7 问题6：全信息测度不能用来度量日常语义信息或优化机器学习

日常语义信息比如：天气预报、股市预测、时钟、温度表、GPS指针…提供的信息。怎样用全信息公式度量这些信息，钟义信从来没有解释过。机器学习中常用正则化失真准则是适用的，也很好理解；而全信息准则和这些准则相差很远，也难以理解。，

尽管钟义信提出机制主义人工智能，说要把信息科学理论或全信息理论作为人工智能的理论基础，但是却没有说明怎样用全信息准则优化机器学习，比如优化多标签学习和分类。机器学习通常使用最大似然、最小交叉熵或最小KL距离、正则化最小失真、最小变分自由能…准则。我们也可以使用最大语义信息准则【6】, 因为它等价于最大似然准则和最小变分自由能准则并兼容正则化最小失真准则。而最大全信息准则和这些准则完全不兼容，谁也不知道如何使用全信息准则优化学习函数或预测模型。相比之下，G理论已经成功应用于多标签学习，最大互信息分类，混合模型，求解隐含变量，改进变分贝叶斯，改进贝叶斯确证【6】，改进最小自由能原理为最大信息效率原理【13】。

4. 全信息理论问题多的原因

4.1研究路线特殊

语义信息论研究路线表现在两方面：

1）    是在香农信息论基础上推广，还是建立一个完全不同的语义信息论。

钟义信选择的是后者。具体表现在，他连条件概率和互信息公式都不使用。

2）    是否使用逻辑概率和真值函数。这可以分为下面几种：

l  仅仅使用逻辑概率而不用真值函数——如Carnap和Bar-Hillel【8】，其语义信息公式是：语义信息=log(1/逻辑概率)。

l  只用真值函数，不使用逻辑概率。这是钟义信的选择。

l  兼用逻辑概率和真值函数，除了使用真值函数构成的模糊熵，还使用逻辑概率构成的语义熵——最近兴起的方法【12】。

l  兼用统计概率、逻辑概率和真值函数——这是我的方法，其中模糊熵H(Y_θ|X)（多语句模糊熵）和语义熵H(Y_θ)中log左边的函数仍然是统计概率，反映信源和香农信道，用于求平均【6】。

钟义信选择的路线非常特殊，就是使用真值函数构造模糊熵（单语句模糊熵），在模糊熵基础上——而不是在香农信息论基础上——定义语法，语义和语用信息。所以他得到的全信息理论和香农信息论差距太远，难以理解。

4.3 追求理论形式的统一性，缺少实用考虑

从公式1-8可以看出，钟义信想用一种形式的公式度量各种信息，但是却没有考虑它们用在哪里，用起来是否合理。如果考虑实用，他应该能得到图1，并发现其中问题。其语用信息公式更是没有考虑实用意义，比如信息带来的价值。

信息论的价值在于优化通信，语义信息论的主要意义在于优化语义通信。而在全信息理论中，我们看不到优化方法。

4.4 缺少同行交流

如果钟义信能经常和同行交流，应该也能很快发现图1所示问题。但是直到2018年，我在微信群里告诉他这个问题时他才知道。此后他表示：度量语义信息是困难的，甚至是不可能的，因为涉及语用；定性讨论语义信息就行了。但是，他走的路线不成功，别的路线未必就不能成功。

5. 结束语

钟义信对中国信息科学研究起到很大的促进作用，但是其《信息科学原理》核心部分——全信息理论——存在许多问题，这些问题包括：语义信息量在说对说错时一样多，而且和逻辑概率无关；语义信息测度没有编码意义，和香农信息论不兼容，和机器学习中常用的优化准则也不兼容，很难用于实践。主要原因是：研究路线特殊——只使用真值和模糊熵而不使用逻辑概率和条件概率；缺少和同行交流。作为前信息论学会会长，钟义信没有促进信息科学研究的百花齐放，这导致同行缺少交流。

最近，国际开放期刊Entropy出了一期以中国学者为主的专刊《语义信息论》【14】，这是一个很好现象。希望新的信息论学会和信息科学研究组织能总结经验教训，让中国的语义信息论和信息科学研究不再是自说自话，而是百家争鸣。

6. 参考文献

【1】钟义信，信息科学原理（第五版），北京邮电大学出版社，2013.

【2】Claude E. Shannon, Warren Weaver. The Mathematical Theory of Communication, The University of Illinois Press: Urbana, IL, USA, 1963.

【3】钟义信， A Theory of Semantic Information. Proceedings 2017, 1, 129. https://doi.org/10.3390/IS4SI-2017-04000

【4】李宗荣，田爱景，关于钟义信院士全信息概念与广义信息论的评析，2025年武汉信息科学研讨会.

【5】鲁晨光，语义信息论专著和文章，http://www.survivor99.com/lcg/books/GIT/

【6】鲁晨光，A Semantic Generalization of Shannon’s Information Theory and Applications, Entropy 2025, 27(5),461; https://doi.org/10.3390/e27050461.中文版:http://www.survivor99.com/LCG/information/Improve/

【7】牛凯，张平， A mathematical theory of semantic communication, 通信学报，2024, 45,8-59.

【8】Rudolf Carnap, Yehoshua Bar-Hillel. An Outline of a Theory of Semantic Information; Tech. Rep. No. 247; Research Laboratory of Electronics, MIT: Cambridge, MA, USA, 1952.

【9】Kenneth J. Arrow. The Economics of Information: An Exposition. Empirica 1996, 23, 119–128. https://doi.org/10.1007/BF00925335

【10】Thomas M. Cover, Joy A. Thomas. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 2006.

【11】鲁晨光，投资组合的熵理论和信息价值，中国科技大学出版社，1997.

【12】Gangtao Xin，Pingyi Fan，Khaled B. Letaief， Semantic Communication: A Survey of Its Theoretical Development. Entropy 2024, 26, 102. https://doi.org/10.3390/e26020102

【13】鲁晨光，Improving the Minimum Free Energy Principle to the Maximum Information Efficiency Principle，Entropy,2025,27(7),684; https://doi.org/10.3390/e27070684. 中文版：http://www.survivor99.com/LCG/information/Improve/

   【14】Entropy: Special issue: Semantic Information Theory，2025，https://www.mdpi.com/journal/entropy/special_issues/Z5DLC3A359